
Photographs & Text adapted from Photobit
RGB "Bayer" Color
and MicroLenses
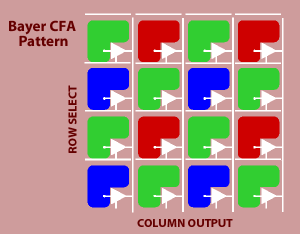
Bayer
color filter array is a popular format for digital acquisition of color images
[1]. The pattern of the color filters is shown below. Half of the total number
of pixels are green (G), while a quarter of the total number is assigned to both
red (R) and blue (B).
|
G |
R |
G |
R |
|
B |
G |
B |
G |
|
G |
R |
G |
R |
|
B |
G |
B |
G |
In order to obtain this color information, the color image sensor is covered with either a red, a green, or a blue filter, in a repeating pattern. This pattern, or sequence, of filters can vary, but the widely adopted “Bayer” pattern, which was invented at Kodak, is a repeating 2x2 arrangement.


Photographs
& Text adapted from Photobit
When the image sensor is read out, line by line, the pixel sequence comes out GRGRGR, etc., and then the alternate line sequence is BGBGBG, etc. This output is called sequential RGB (or sRGB).
Since each pixel has been made sensitive only to one color (one spectral band), the overall sensitivity of a color image sensor is lower than a monochrome (panchromatic) sensor, and in fact is typically 3x less sensitive. As a result, monochrome sensors are better for low-light applications, such as security cameras. (It is also why human eyes switch to black and white mode in the dark).
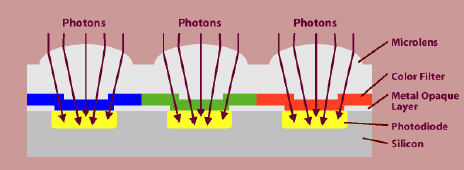
MicroLenses
Microlenses and a metal opaque layer above the silicon funnel light to the photo-sensitive portion of each pixel. On their way, the photons of light pass through a color filter array (CFA) where the process begins of obtaining color from the inherently “monochrome” chip. (Actually, “panchromatic” is an apter term, since sensors respond across the spectrum; the word monochrome comes from television use and refers to black and white).
White
Balance, Bayer Interpolation and Color matrix Processing
White Balance and Color Correction are processing operations performed to ensure proper color fidelity in a captured digital camera image. In digital cameras an array of light detectors with color filters over them is used to detect and capture the image. This sensor does not detect light exactly as the human eye does, and so some processing or correction of the detected image is necessary to ensure that the final image realistically represents the colors of the original scene.
|
G |
R |
G |
R |
|
B |
G |
B |
G |
|
G |
R |
G |
R |
|
B |
G |
B |
G |
Each pixel only
represents a portion of the color spectrum and must be interpolated to obtain an
RGB value per pixel. The Bayer color filter array (CFA) pattern, shown above, is a popular format
for digital acquisition of color images [1]. Half of the total number of pixels
are green (G), while a quarter of the total number is assigned to both red (R)
and blue (B).
This note describes conversions from Bayer format data to RGB and between RGB and YUV (YCrCb) color spaces. We also discuss two color processing operations (white balance and color correction) in the RGB domain, and derive the corresponding operations in the YUV domain. Using derived operations in the YUV domain, one can perform white balance and color correction directly in the YUV domain, without switching back to the RGB domain.
1.) White Balance & Bayer
Interpolation
The
first step in processing the raw pixel data is to perform a white balance
operation. A white object will have
equal values of reflectivity for each primary color: ie:
R
= G = B
An
image of a white object can be captured and its histogram analyzed. The color channel that has the highest level is set as the
target mean and the remaining two channels are increased with a gain multiplier
to match. For example, if Green
channel has the highest mean, gain ‘a’ is applied to Red and gain ‘b’ is
applied to Blue.
G’
= R’a = bB’
The White Balance will vary, based on the color lighting source (Sunlight, Fluorescent, Tungsten) applied to the object and the amount of each color component within it. A full color natural scene can also be processed in the same fashion. This “Gray World” method assumes that the world is gray and the distribution of primaries color will be equal.
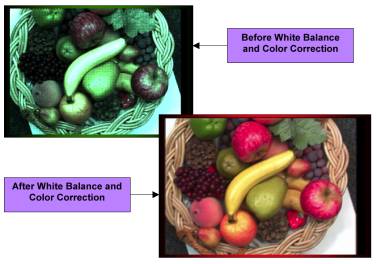
The
“White Patch” method attempts to locate the objects that are truly white,
within the scene; by assuming the whites pixels are also the brightest (I =
R+G+B). Then, only the top
percentage intensity pixels are included in the calculation of means, while
excluding any pixels that may have any channel that is saturated.
To convert an image from the bayer format to an RGB per pixel format, we need to interpolate the two missing color values in each pixel. Several standard interpolation methods (nearest neighbor, linear, cubic, cubic spline, etc.) were evaluated on this problem in [2]. The authors have measured interpolation accuracy as well as the speed of the method and concluded that the best performance is achieved by a correlation-adjusted version of the linear interpolation. The suggested method is presented here.
(a) |
(b) |
||||||||||||||||||
(c) |
(d) |
Figure
1: Four possible cases for interpolating R and B components
As suggested in [2], R and B values are
interpolated linearly from the nearest neighbors of the same color. There are
four are possible cases, as shown in Figure 1. When interpolating the missing
values of R and B on a green pixel, as in Figure 1 (a) and (b), we take the
average values of the two nearest neighbors of the same color. For example, in
Figure 1 (a), the value for the blue component on a shaded G pixel will be the
average of the blue pixels above and below the G pixel, while the value for the
red component will be the average of the two red pixels to the left and right of
the G pixel.
Figure 1 (c) shows the case when the value of the blue component is to be interpolated for an R pixel. In such case, we take the average of the four nearest blue pixels cornering the R pixel. Similarly, to determine the value of the red component on a B pixel in Figure 2 (d) we take the average of the four nearest red pixels cornering the B pixel.
Interpolating the green component
By [2],
green component is adaptively interpolated from a pair of nearest neighbors. To
illustrate the procedure, consider two possible cases in Figure 2.
(a) |
(b) |
Figure
2: Two possible cases for interpolating G component
In
Figure 2 (a), the value of the green component is to be interpolated on an R
pixel. The value used for the G component here is
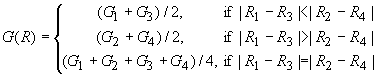
In other words, we take into account the
correlation in the red component to adapt the interpolation method. If the
difference between R1 and R3 is smaller than the
difference between R2 and R4, indicating that the
correlation is stronger in the vertical direction, we use the average of the
vertical neighbors G1 and G3 to interpolate the required
value. If the horizontal correlation is larger, we use horizontal neighbors. If
neither direction dominates the correlation, we use all four neighbors.
Similarly, for Figure 2 (b) we will have
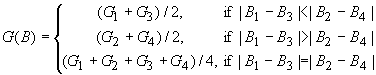
To
conclude this section, note that if the speed of execution is the issue, one can
safely use simple linear interpolation of the green component from the four
nearest neighbors, without any adaptation
![]()
According to [2], this method of interpolation executes twice as fast as the adaptive method, and achieves only slightly worse performance on real images. For even fast updates only two of the four green values are averaged. However, this method displays false color on edges or zipper artifacts.
Color Saturation Matrix
The operation
for saturation can be applied at the same time as the color correction matrix.
Unlike the color correction matrix, the saturation matrix does not rotate
the vectors in the color wheel:
|
[m00 m01
m02] [ R ] |
m00 = 0.299 +
0.701*K |
m10 = 0.299 *
(1-K) |
m20 = 0.299 *
(1-K) |
K
is the saturation factor
K=1 means no change
K > 1 increases saturation
0<K<1 decreases saturation, K=0
produces B&W , K<0 inverts
color
A sample
table of matrix values are calculated and shown below:
|
|
|
Saturation |
Saturation |
Saturation |
Saturation |
|
|
|
1 |
1.7 |
1.9 |
2 |
|
R’
= |
+R* |
1.0 |
1.4907 |
1.6309 |
1.701 |
|
|
+G* |
0 |
-0.4109 |
-0.5283 |
-0.587 |
|
|
+B* |
0 |
-0.0798 |
-0.1026 |
-0.114 |
|
|
|
|
|
|
|
|
G’
= |
+R* |
0 |
-0.2093 |
-0.2691 |
-0.299 |
|
|
+G* |
1.0 |
1.2891 |
1.3717 |
1.413 |
|
|
+B* |
0 |
-0.0798 |
-0.1026 |
-0.114 |
|
|
|
|
|
|
|
|
B’
= |
+R* |
0 |
-0.2093 |
-0.2691 |
-0.299 |
| |
+G* |
0 |
-0.4109 |
-0.5283 |
-0.587 |
|
|
+B* |
1.0 |
1.6202 |
1.7974 |
1.886 |
The saturated image can be further processed with an additional color
correction matrix to compensate for cross-talk induced by the micro-lens and
color filter process, lighting and temperature effects.
The combination matrix ([color correction matrix] *
[saturation matrix]) results in a closer to true world color
representation, but an increase in noise. Typically,
the blue pixel has the lowest pixel response and the highest Crosstalk from the
Green and Red light. The resulting
noise after matrix operation is a high degree of blue noise.
A monochrome image can now be easily obtained from a color image by setting K=0
|
m00 = 0.299 m01 = 0.587 m02 = 0.114 |
m10 = 0.299 m11 = 0.587 m12 =
0.114 |
m20 = 0.299 m21 = 0.587 m22 =
0.114 |
2. Conversion between RGB and YUV
We give two commonly used forms of equations for conversion between RGB and YUV formats. The first one is recommended by CCIR [3]
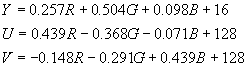 (2.1)
(2.1)
The second form is used by Intel in their
image processing library [4], and may be more suitable for implementation:
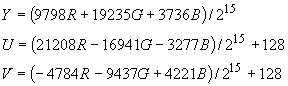
In either case, resulting values of Y, U and V should be clipped to fit the appropriate range for the YUV format (e.g. [0,255] for a 24-bit YUV format). The inverse conversion may be accomplished by:
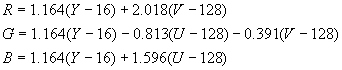
3. White balance operation in RGB and YUV domains
The white balance operation is defined as a gain correction for red, green and blue components by gain factors AR, AG and AB, respectively, i.e.
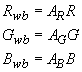
The new (white-balanced) values for red, green and blue are Rwb, Gwb and Bwb. To derive the equivalent form of this operation in the YUV domain, we proceed as follows. First, write equation (2.1) as
![]() (3.2)
(3.2)
where
![]() is the vector in the RGB space,
is the vector in the RGB space,
![]() is the corresponding vector in the
YUV space,
is the corresponding vector in the
YUV space,
![]() , and C is the appropriate matrix of conversion coefficients. Similarly,
(3.1) can be written as
, and C is the appropriate matrix of conversion coefficients. Similarly,
(3.1) can be written as
![]() (3.3)
(3.3)
where
![]() is the vector in the RGB space
modified by white balance operation (2.4), and
is the vector in the RGB space
modified by white balance operation (2.4), and
![]() . We want to determine what is the corresponding vector
. We want to determine what is the corresponding vector
![]() in the YUV domain, without having to revert back to the RGB domain. Vector
in the YUV domain, without having to revert back to the RGB domain. Vector
![]() is found by substituting
is found by substituting
![]() for x in (3.2)
for x in (3.2)
![]() .
.
Let
![]() , so that
, so that
![]() . Then
. Then
![]() . Substitute this expression for x back into (3.2) to obtain:
. Substitute this expression for x back into (3.2) to obtain:
![]() (3.4)
(3.4)
This equation provides the connection between
y and
![]() without involving x or
without involving x or
![]() (i.e. without going back to the RGB
domain). Manipulating (3.4) and using the fact that for nonsingular matrices
(i.e. without going back to the RGB
domain). Manipulating (3.4) and using the fact that for nonsingular matrices
![]() [5], we get that white balance
operation in the YUV domain is
[5], we get that white balance
operation in the YUV domain is
![]() (3.5)
(3.5)
Expressing components of
![]() from (3.5) we get
from (3.5) we get
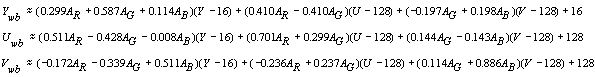
Terms with leading coefficient less than 10-3 have been dropped.
References
[1] B. E. Bayer, Color imaging array, US Patent No. 3971065.
[2] T. Sakamoto, C. Nakanishi and T. Hase, “Software pixel interpolation for digital still cameras suitable for a 32-bit MCU,” IEEE Trans. Consumer Electronics, vol. 44, no. 4, November 1998.
{3} http://www.northpoleengineering.com/rgb2yuv.htm